SILICOM CONNECTIVITY SOLUTIONS, INC.
ETHERMODEM/SEM14 (ETHERNET + 14.4KBPS MODEM)
|
Card Type |
Fax, Modem (synchronous/asynchronous), Network Interface Card |
|
Chip Set |
Unidentified |
|
I/O Options |
Ethernet 10Base2 connector, Ethernet 10BaseT connector |
|
NIC Type |
Ethernet |
|
Network Transfer Rate |
10Mbps |
|
Maximum Modem Rate |
14.4Kbps |
|
Maximum Fax Rate |
14.4Kbps |
|
Data Bus |
PCMCIA Type II |
|
Fax Class |
Class I & II |
|
Data Modulation Protocol |
Bell 103/212A ITU-T V.21, V.22, V.22bis, V.23, V.32, V.32bis |
|
Fax Modulation Protocol |
ITU-T V.17, V.21CH2, V.27ter, V.29 |
|
Error Correction/Compression |
MNP5, MNP10, V.42, V.42bis |
|
Topology |
Linear Bus, Star |
|
Wiring Type |
Unshielded twisted pair RG-58A/U 50ohm coaxial |
|
Boot ROM |
Not available |

|
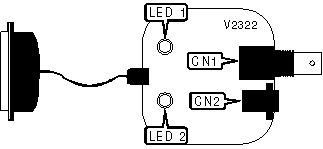
CONNECTIONS | ||||||
|
Function |
Label |
Function |
Label | |||
|
10BASE-2 - RG-58A/U 50ohm coaxial |
CN1 |
10BASE-T - Unshielded twisted pair |
CN2 | |||
|
DIAGNOSTIC LED(S) | |||
|
LED |
Color |
Status |
Condition |
|
LED 1 |
Yellow |
On |
Link integrity good on 10BASE-T connection |
|
LED 1 |
Yellow |
Off |
Link integrity broken on 10BASE-T connection |
|
LED 2 |
Green |
Blinking |
Sending or receiving data |
|
LED 2 |
Green |
Off |
Not sending or receiving data |
|
SUPPORTED COMMAND SET |
|
Basic AT Commands |
|
AT, ‘Comma’, A/ |
|
A, B, C, D, E, H, L, M, N, O, P, Q, S, T, V, W, X, Y, Z |
|
&C, &D, &F, &G, &J, &K, &L, &M, &P, &Q, &R, &S, &T |
|
&V, &W, &X, &Y, &Z |
|
Extended AT Commands |
|
\A, \B, \G, \K, \L, \N, %C, %E, %l, %Q, %TT |
|
S Registers |
|
S0, S1, S2, S3, S4, S5, S6, S7, S8, S9, S10, S11, S12, S16, S18, S25, S26, S29, S30 |
|
S32, S33, S37, S38, S39, S46, S48, S82, S86, S91, S92, S95, S99, S201 |
|
Special Commands |
|
)M, *H, -K, -Q, @M, :E, #CID |
|
Note: See MHI Help file for full command documentation. |
Proprietary AT Command Set
See SILICOM CONNECTIVITY SOLUTIONS, INC.,ETHERMODEM/SEM28 (ETHERNET + 28.8KBPS MODEM) document for a full command summary.